Sistemas de Numeración.

Sistemas de Numeración.

Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos. Un sistema de numeración puede representarse como:

${\displaystyle {\mathcal {N}}=(S,{\mathcal {R}})}$

donde:

• ${\displaystyle {\mathcal {N}}}$ es el sistema de numeración considerado (p.ej. decimal, binario, hexadecimal, etc.).

• ${\displaystyle S\,}$ es el conjunto de símbolos permitidos en el sistema. En el caso del sistema decimal son {0,1,...9}; en el binario son {0,1}; en el octal son {0,1,...7}; en el hexadecimal son 0,1,...9,A,B,C,D,E,F.

• ${\displaystyle {\mathcal {R}}}$ son las reglas que nos indican qué números y qué operaciones son válidos en el sistema, y cuáles no. En un sistema de numeración posicional las reglas son bastante simples, mientras que la numeración romana requiere reglas algo más elaboradas.

Los sistemas de numeración utilizan principalmente cuatro tipos de representaciones fundamentales para el significado de estas, los cuales son : Binario, Decimal, Octal y Hexadecimal.

Sistema Binario.

El sistema binario, llamado también sistema diádico​ en ciencias de la computación, es un sistema de numeración en el que los números se representan utilizando solamente dos cifras: cero y uno (0 y 1). Es uno de los sistemas que se utilizan en las computadoras, debido a que estas trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario.

Ejemplo.

Convierte el numero 151 decimal a binario 

  20=   1|1
  21=   2|1
  22=   4|1
  23=   8|0
  24=  16|1
  25=  32|0
  26=  64|0
  27= 128|1           ${\displaystyle 128+16+4+2+1=(151)_{10}=(10010111)_{2}}$

Sistema Decimal.

El sistema de numeración decimal, también llamado sistema decimal, es un sistema de numeración posicional en el que las cantidades se representan utilizando como base aritmética las potencias del número diez.

---

Cambio de base 10 a base 8

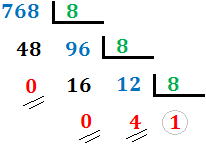
Veamos el método para pasar del sistema decimal al sistema octal mediante un ejemplo. Escribiremos el número ${768}_{(10}$ (base 10) en base 8:

1. Dividimos el número entre 8:
   
   
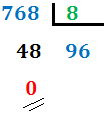
2. Si el cociente es mayor o igual que 8, lo dividimos entre 8.
   En nuestro caso, el cociente es 96 (mayor que 8), por lo que lo dividimos de nuevo:
   
   
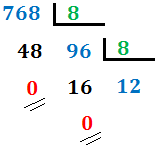
3. Continuamos así hasta obtener un cociente menor que 8.
   En nuestro caso, el cociente es 12 (mayor que 8), así que lo dividimos de nuevo:
   
   
   El cociente es 1, menor que 8, con lo que hemos terminado el proceso. Hemos indicado los restos con dos rayas y el último cociente con una circunferencia.
4. El número en base 8 es:
   (Último cociente) (Último resto) (Penúltimo resto)... (Segundo resto) (Primer resto).
   En nuestro caso,
   
   • El último cociente es 1.
   • El último resto es 4.
   • El penúltimo resto es 0.
   • El primer resto es 0.
   Por tanto, el número 768 en base octal es 1400. Es decir,
   
   

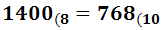
Sistema Octal.

El sistema numérico en base 8 se llama octal y utiliza los dígitos del 0 al 7. En informática a veces se utiliza la numeración octal en vez de la hexadecimal. Tiene la ventaja de que no requiere utilizar otros símbolos diferentes de los dígitos.

Ejemplo.

Escribir en octal el número decimal 179

179÷8= 22

22= cociente

8 x 22= 176

179-176= 3

3= residuo

22÷8= 2

2=cociente

8x2= 16

22-16= 6

6= residuo

2÷8= 0

0= cociente

8x0= 0

2-0= 2

2= residuo

El octal del número decimal 179= 263

Sistema Hexadecimal.

Es el sistema de numeración posicional que tiene como base el 16. En principio, dado que el sistema usual de numeración es de base decimal y, por ello, sólo se dispone de diez dígitos, se adoptó la convención de usar las seis primeras letras del alfabeto latino para suplir los dígitos que nos faltan. El conjunto de símbolos es el siguiente:

${\displaystyle S=\{0,1,2,3,4,5,6,7,8,9,\mathrm {A} ,\mathrm {B} ,\mathrm {C} ,\mathrm {D} ,\mathrm {E} ,\mathrm {F} \}\,}$

Se debe notar que A = 10, B = 11, C = 12, D = 13, E = 14 y F = 15. En ocasiones se emplean letras minúsculas en lugar de mayúsculas. Como en cualquier sistema de numeración posicional, el valor numérico de cada dígito es alterado dependiendo de su posición en la cadena de dígitos, quedando multiplicado por una cierta potencia de la base del sistema, que en este caso es 16. 

Por ejemplo: 3E0A₁₆ = 3×16³ + E×16² + 0×16¹ + A×16⁰ = 3×4096 + 14×256 + 0×16 + 10×1 = 15882.